La cryptographie consiste à rendre un texte incompréhensible sauf par un destinataire qui connaît la façon de le rendre lisible. La cryptanalyse consiste à déchiffrer un texte crypté pour lui rendre son sens. Les deux techniques sont complémentaires car si la personne qui reçoit le document encrypté ne peut pas le décrypter cela ne sert à rien.
Le but de ce document n’est pas d’effectuer une analyse exhaustive de ces sciences qui s’avèrent être fort complexes, il y a des ouvrages pour cela, mais de fournir quelques éléments de compréhension relatifs aux techniques employées, à l’historique de l’écriture secrète et aussi, pourquoi pas, donner matière à distraction. Les jeunes adorent les codes secrets, cela leur permet de rêver, de jouer aux espions ou de découvrir des trésors cachés ! Et quand je dis les jeunes…
Parlons peu mais parlons bien.
Avant d’entrer dans le vif du sujet nous allons effectuer une digression relative au langage parlé secret.
La façon la plus simple de le faire consiste à parler une langue différente! Mais bien entendu il y a toujours eu des interprètes, y compris dans l’antiquité.
Pendant la guerre du Pacifique les Américains ont utilisé des soldats de la tribu indienne des Navajos dont le langage n’est compris que par eux même ! Ils ont dû inventer des mots pour désigner les systèmes militaires inconnus par leur peuple, comme les sous-marins (Poissons de fer) ou les bombardiers (Buses), les différentes unités de l’armée, les grades etc.
Et les « messages personnels » de la BBC me direz-vous ? Il s’agit de phrases n’ayant aucun rapport avec leur signification habituelle, les linguistes diront que le signifiant et le signifié sont différents. C’est une méthode très rudimentaire : cela nécessite une phrase par action à mener, prévue à l’avance. Ces phrases sont des déclencheurs ou des avertisseurs, des boutons-poussoirs.
On parle alors de langage codé. Le chiffrage de la parole n’est advenu que lorsqu’on a su la numériser dans les années 1980. L’Armée française s’est largement distinguée en ce domaine.
Les « codes » Morse, ASCII, Baudot ne sont pas secrets, ce sont des alphabets destinés à être utilisés par des MACHINES. En revanche les signaux du télégraphe de CHAPPE sont bien codés car il faut posséder le « livre de codes » pour comprendre la signification des nombres successifs représentés par la position des bras. Cela peut être des lettres, des mots ou des phrases entières.
De la même façon les hiéroglyphes, les caractères cunéiformes, aztèques et nombre d’autres alphabets tels que l’arabe, l’hébreu ainsi que les idéogrammes chinois etc. ne sont pas des codes, ils constituent une façon d’écrire différente de celle que nous avons héritée des Romains.
Dans un message CODÉ un mot en remplace un autre convenu à l’avance alors qu’un message CHIFFRÉ voit les lettres qui le composent remplacées par d’autres. (On dit aussi message crypté ou encrypté).
Billets doux et antisèches : la stéganographie !
Le moyen le plus simple de garder un texte secret est de le dissimuler à la vue, c’est ce que font les amoureux et les cancres, mais il ne faut pas se faire prendre ! De nos jours cela n’a plus vraiment cours ou alors sous une forme… électronique, SMS, téléphones à cartes prépayées, mémoires des calculatrices etc.
Rien de cela au temps des guerres médiques entre les Perses et les Grecs au Ve siècle avant Jésus-Christ! On utilisait la stéganographie qui veut dire simplement : « écriture dissimulée ».
Hérodote raconte dans ses « Histoires » que le monarque Xerxès avait décidé de conquérir la Grèce et rassemblé une grande armée en ce but. Ses plans furent dévoilés grâce à un message caché et les Grecs furent victorieux lors de la bataille navale de Salamine. L’espion des Grecs, Demarate[1], avait ôté la cire de tablettes, écrit sur le bois puis remis de la cire. Les plaquettes vierges de toute écriture furent transmises sans encombre et Gorgô, l’épouse de Léonidas[2], aurait eu l’idée de racler la cire, faisant apparaître ainsi le message salvateur. Si les Perses avaient été victorieux et envahi la Grèce certains historiens pensent que cela aurait considérablement ralenti le développement de la civilisation occidentale.
On raconte également qu’un homme se fit raser la tête où l’on écrivit un message. Après repousse des cheveux il put passer sans être inquiété et il suffit alors de lui raser la tête à nouveau. César, pour avertir des troupes assiégées aurait fait lancer contre leur palissade un javelot dont la virole contenait un message.
Les histoires de messages galants ou autres cachés un peu partout abondent et de nombreux films relatant la seconde guerre mondiale montrent des jeunes filles cachant des papiers enroulés à l’intérieur des tubes du cadre de leur vélo, les sentinelles allemandes, sans doute peu formées à l’espionnage, s’intéressant davantage à leurs corsages qu’à autre chose.
L’ « encre sympathique » est un autre exemple de stéganographie connu depuis l’Antiquité. Elle est décrite par Pline l’Ancien qui utilisait le latex de l’Euphorbe. Le jus de citron ou l’urine conviennent comme la plupart des liquides carbonés transparents.
Au XXe siècle on sut réaliser des microfilms faciles à dissimuler et des micropoints disposés sur des « i » ou remplaçant les notes noires d’une portée musicale, moyens permettant la transmission de plans, ce que la cryptographie ne permettait pas encore. De nos jours, avec la numérisation des images et des sons, tout s’encrypte communément.
L’écriture cachée peut être ludique, par exemple sous la forme de l’acrostiche. Je me souviens d’un « grand jeu » scout où il fallait déchiffrer un message secret indiquant l’endroit où l’on devait se rendre afin de continuer le parcours. Le message était : « Dans Un Nœud Efficace ». Vous avez trouvé, il fallait aller sur la DUNE ! Les enfants adorent ça et il y a davantage de plaisir à composer un acrostiche qu’à le déchiffrer. Il y en a de célèbres, parfois grivois ! Consultez Wikipédia sur INTERNET…
Une autre forme de codage consiste à remplacer les lettres latines par un autre alphabet, Grec, Cyrillique ou des symboles inventés, des « hommes dansants » dans le roman de Conan Doyle ou le chiffre de Marie reine d’Ecosse dont le décodage lui coûta la vie ainsi qu’aux conspirateurs !
Nota : Une épreuve (non verbale) d’un test célèbre propose de décoder un texte représenté par des symboles. La personne testée dispose de la correspondance entre lettres et symboles, il n’y a donc aucune difficulté à décoder, mais l’épreuve est chronométrée. Le but est d’évaluer la mémoire visuelle: si l’on se souvient de la correspondance entre les symboles et des lettres fréquemment utilisées on va beaucoup plus vite. L’examinateur peut également évaluer la stratégie : soit le candidat rempli la grille lettre par lettre soit il remplit toutes les cases contenant le même symbole.
Après avoir envisagé l’écriture cachée, nous allons envisager l’écriture brouillée, incompréhensible. Nous pouvons nous affranchir rapidement de l’écriture codée que nous venons d’évoquer lorsque les mots ou les phrases n’ont pas leur signification habituelle. Le « code Q » des radios civils ou le « code Z » des militaires en fait partie. Le but n’est pas de rendre le message incompréhensible mais de le raccourcir : ce sont des abréviations. Etant connus internationalement ils permettent de fait une meilleure compréhension entre interlocuteurs ne parlant pas la même langue : « QRZ ? » signifie « Qui appelle ?» partout dans le monde.
La cryptographie répond depuis toujours à quelques principes.
La cryptographie est sans doute aussi ancienne que l’écriture et elle est liée à des besoins de confidentialité civils ou militaires. Il s’agit de transformer un texte dit « clair » en un texte « chiffré ». Elle s’applique au niveau des lettres, pas au niveau des mots ou des phrases.
Quelque soit la façon de procéder il faudra procéder à la déstructuration de la phrase. En effet en Français il est facile de repérer les mots d’une, de 2 ou 3 lettes ! Très souvent on constate que les messages secrets se composent de groupes égaux de 5 lettres.
Il y a deux types principaux de chiffrage : la transposition et la substitution.
- La transposition déplace les lettres du texte. De ce fait le message crypté contiendra toutes les lettres du message clair dans le désordre ;
- La substitution : le chiffrage remplace les lettres par d’autres, parfois toujours la même et parfois non ce qui complique énormément la cryptanalyse. Le codage est une forme de substitution où ce sont les mots et parfois les phrases qui ne sont plus les mêmes.
La transposition
La transposition dispose les lettres d’un texte de façon différente mais en suivant une logique précise afin que le correspondant puisse rétablir le message en langage clair.
Il ne faut pas la confondre avec une anagramme qui consisteà modifier la place des lettres d’un mot pour en créer un autre souvent dans un but amusant. Par exemple André Breton[3] avait transformé « Salvador Dali » en « Avida Dollars » ! Les candidats du jeu « Des chiffres et des lettres » tentent de résoudre des anagrammes. Mais dans cet exercice il n’y a pas de logique au changement de disposition et cela ne pourrait pas constituer des messages secrets. Toutefois les amateurs d’anagrammes ont des facilités intellectuelles pour les décoder, tout comme les cruciverbistes. Alan Turing en utilisait dans son équipe de Bletchley Park pour briser les secrets de la machine ENIGMA.
Voici quelques exemples de transpositions.
La « dent de scie » consiste à écrire une phrase sur deux lignes de longueur égale puis à prendre alternativement les lettres de l’une et de l’autre : « Les lecteurs de Radiofil aiment les codes secrets »
L E S L E C T E U R S D E R A D I O F I L
A I M E N T L E S C O D E S S E C R E T S
L A E I S M L E E N C T T L E E U S R C S O D D E E R S A S D E I C O R F E I T L S
Soit : LAEIS MLEEN CTTLE EUSRC SODDE ERSAS DEICO RFEIT LS
Si le nombre de lettres est impair ajouter une lettre inutile à la fin. Pour décrypter on écrit la première lettre sur une ligne, la seconde en-dessous et ainsi de suite. On peut compliquer l’affaire en séparant les lettres deux par deux ou toute combinaison convenue entre les correspondants : ce sera la clef. Le fait d’écrire sur deux lignes s’appelle l’algorithme. Dans tous les types d’encryptage, même les plus sophistiqués, il y a toujours un algorithme et une clef : La machine ENIGMA crée un algorithme et la clef se trouve dans un « livre de connaissance des groupes »[4] lesquels changent chaque jour.
L’encryptage avec la scytale

date de l’époque des guerres entre Sparte et la Perse. C’est le premier exemple de cryptage militaire par transposition connu. Il s’agit d’un bâton sur lequel on enroule en hélice à spires jointives une bande de cuir ou de parchemin. On écrit le message lettre à lettre horizontalement sur plusieurs lignes.
Lorsque la bande est déroulée toutes les lettres sont décalées et on ne comprend plus ce qu’il y a d’écrit.
En enroulant à nouveau la bande sur un bâton de même diamètre (ce qui constitue la clef) le texte reprend son sens. Cela revient à décaler chaque lettre du nombre de lettres que l’on place sur une spire.
On peut s’amuser à reproduire le système avec un tube de PVC et un ruban de « bolduc » qui sert à décorer les paquets cadeau.
La substitution.
Comme son nom l’indique consiste à remplacer une lettre par une autre. Elle peut être simple avec un remplacement unique ou beaucoup plus complexe pour en arriver aux diverses machines à crypter.
Le chiffre dit « de César » est le plus connu. Il est à la portée des enfants d’école primaire. Il s’agit de décaler dans l’alphabet (algorithme) les lettres d’un certain nombre de rangs et dans un sens ou dans l’autre (clef). Par exemple A devient B, B devient C et Z devient A. Ce chiffre qui a dû avoir de l’efficacité à l’époque antique où peu de gens savaient lire peut servir uniquement à un jeu enfantin à notre époque.
Exemple : RADIOFIL MAGAZINE devient : SBEJPGJM NBHBAJOF.
Remplacer l’alphabet romain par le grec devait en accroître l’efficacité. Nous pourrions « coder » chaque lettre avec des symboles pour le complexifier.
Le chiffrage par substitution simple a une grande faiblesse. Chaque lettre du texte en clair est toujours représentée par la même lettre cryptée.
Or on sait que dans chaque langue la fréquence d’utilisation d’une lettre est connue. Il suffit de regarder la casse d’un typographe pour constater que le casier contenant les « e » est bien plus important que les autres. En effet il y a environ 16% de « e » dans un texte en Français, « k » et « w » sont quasi absents. En se basant sur ces statistiques on peut débuter le décryptage à la condition que le texte soit assez long pour qu’elles puissent s’appliquer opportunément.
Le carré de Vigenère[5] est beaucoup plus sécurisé même s’il ressemble au chiffre de César. Chaque lettre est substituée sur le même principe mais l’alphabet de substitution change à chaque fois en suivant une clef. C’est une substitution poly-alphabétique qui résiste à l’analyse de fréquence des lettres.
Ce « carré » est composé de 27 lignes sur 26 colonnes.
La première ligne est constituée par l’alphabet ordinaire dans lequel on puisera les lettres à chiffrer.
Les 26 lignes suivantes sont constituées d’alphabets décalés d’une lettre : le premier commence par B, le second par C et ainsi de suite. Le dernier est un alphabet normal, ce qui veut dire qu’une lettre peut être chiffrée par elle-même, ce qui n’est pas le cas du chiffre de César.
Chacune des lignes commence donc par une lettre différente et la clef désignera quelles lignes il faut utiliser.
Sur l’exemple de graphique ci-dessous les lettres à coder sont inscrites sur la première ligne en minuscules. Je n’ai pas complété le carré jusqu’au bout car ce n’est pas utile pour l’explication.
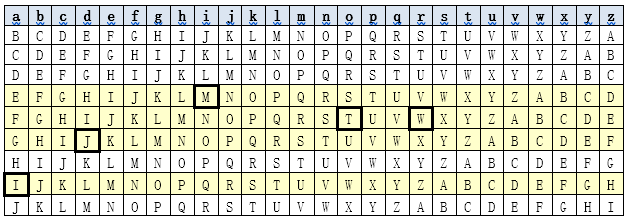
… Et ainsi de suite.
Exemple : Je veux chiffrer : RADIO avec la clef « FIGE »
Le premier « R » se transforme en « W » sur la ligne correspondant à la première lettre de la clef, soit la ligne qui commence par « F ».
« A » sera « I » sur la ligne « I »
« D » sera « J » sur la ligne « G »
« I » sera « M » sur la ligne « E »
« 0 » sera « T » sur la ligne « F » car je recommence après avoir utilisé toutes les lettres de la clef.
Donc RADIO deviendra WIJMT. Le décryptage est aisé : je cherche « W » sur la ligne « F » et cela m’indique la colonne « r », c’est très simple… quand on connait la clef !
Le premier cryptanalyste capable de déchiffrer le carré de Vigenère fut Charles Babbage[6] en 1854.
Le « Grand Chiffre » de Louis XIV et l’homophonie
D’autres méthodes sont apparues par la suite comme la substitution homophonique. Pour déjouer l’analyse des fréquences la même lettre pouvait avoir plusieurs substituts, de plus en plus nombreux en fonction de sa fréquence d’apparition dans les textes. Par exemple « L » pouvait être chiffré en : 26 ou 37, 51, 65, 84, au choix du chiffreur. Au déchiffrement chacun de ces nombres correspondait à cette lettre unique.
Le « Grand Chiffre » de Louis XIV a été créé par Antoine et Bonaventure Rossignol, père et fils, pour encrypter des messages très secrets. Il était tellement élaboré qu’il n’a jamais pu être déchiffré avant la fin du XIXe siècle ! Après la mort du Roi et des inventeurs, le secret s’est perdu. Les historiens ne pouvaient pas prendre connaissance des mystères du règne et en particulier l’histoire du « Masque de fer » ! Le commandant Etienne Bazeries, un cryptographe de l’armée en vint à bout aux environs de 1890. Il découvrit que les nombres ne correspondaient pas à des lettres mais à des syllabes entières et qu’il y avait même des pièges ! (Par exemple un chiffre signifiait qu’il fallait supprimer le précédent.)
Quant au Masque de fer il est possible que ce fût un général félon enfermé à la forteresse de Pignerol qui ne devait sortir de sa geôle qu’avec le visage masqué pour ne pas être reconnu. Mais l’histoire du prétendu jumeau de Louis Dieudonné initiée par Voltaire est tellement plus plaisante que Victor Hugo (Les Jumeaux) ou Alexandre Dumas (Le Vicomte de Bragelonne) l’ont transformée en œuvres littéraires. Les cinéastes ont également exploité ce thème à plusieurs reprises.
Le « code Delastelle[7] » est très abouti. (Référence : « Armement clandestin France » de Pierre LORAIN.)
Ce chiffrage a été utilisé au début de la seconde guerre mondiale par les Alliés. Une seule lettre cryptée par lettre du texte clair, pas de document compromettant mais hélas la clef est en mémoire de l’opérateur qui peut être contraint à la révéler, l’algorithme étant bien connu des cryptanalystes.
| La clef de Violette SZABO, agent du SOE, déportée à Ravensbrück et exécutée en 1944 était : The life that I have Is all that I have And the life that I have Is yours. The love that I have Of the life that I have Is yours and yours and yours. |
Il repose sur la mémorisation par les agents d’une phase personnalisée, souvent quelques vers de poésie pour mieux s’en souvenir[8]. C’est à partir de cette phrase que l’on compose la grille de chiffrage qui se présente sous forme d’un tableau de 5 x 5 lettres, le « W » étant remplacé par deux « V ». On remplit la grille de gauche à droite et de haut en bas avec les lettres de la phrase secrète en prenant garde de ne pas les placer deux fois. Si la grille n’est pas complète, on ajoute les lettres manquantes par ordre alphabétique.
Nous allons prendre comme clef : « Portez ce vieux whisky au juge blond qui fume ». Cette phrase a l’avantage de comporter toutes les lettres de l’alphabet. On s’en servait pour tester les claviers de machines à écrire et vérifier si les touches fonctionnaient toutes correctement.
Composons notre grille avec les lettres de la phrase
| 1 | 2 | 3 | 4 | 5 | |
| 1 | P | O | R | T | E |
| 2 | Z | C | V | I | U |
| 3 | X | H | S | K | Y |
| 4 | A | J | G | B | L |
| 5 | N | D | Q | F | M |
Toutes les lettres y sont (sauf le « W ) et une seule fois. Maintenant chaque lettre est repérable avec deux chiffres par ses coordonnées cartésiennes. On lit de haut en bas et de gauche à droite.
Exemple : V = 32, Q = 35, K = 43.
Nous allons coder : « BONJOUR LES AMIS DE LA CV »
- On commence par faire des groupes de 5 lettres. Si ça ne tombait pas juste on rajouterait des lettres de « bourrage » sans signification, des « X » par exemple.
BONJO URLES AMISD ELACV
- Sous chaque lettre on va placer ses coordonnées VERTICALEMENT.
BONJO URLES AMISD ELACV
42122 53553 15432 55123
41541 21413 45235 14422
- Maintenant on va lire HORIZONTALEMENT dans chacun des groupes de 5 lettres des couples de 2 chiffres.
Exemple : pour le premier groupe cela fait : 42 – 12 – 24 – 15 – 41
Vous notez que l’on prend ensemble le 5ème chiffre de la première ligne et le premier de la seconde ligne.
- On prend maintenant ces couples de chiffres que l’on reporte dans la grille et on obtient les lettres codées : IZJNT à la place de BONJO
- On continue avec les autres groupes de 5 lettres et on obtient à la fin :
IZJNT YMVAX NKJUQ MZRBC - On envoie ces lettres qui composent le message secret…
Et maintenant le décodage de: IZJNT YMVAX NKJUQ MZRBC
- Reprenons la grille et écrivons les coordonnées de chaque lettre du premier groupe de 5 (soit 10 chiffres en tout, 42 – 12- 24 – 15 – 41) en les écrivant HORIZONTALEMENT et en deux lignes de 5 chiffres, soit :
- IZJNT = 42122
41541
Si nous lisons maintenant de façon VERTICALE nous obtenons : 44 – 21 – 15 – 24 – 21
Cela correspond aux lettres : BONJO. Le texte initial est ainsi reconstitué. - Poursuivons le travail pour les autres groupes de 5 lettres afin de décoder tout le message.
Vigenère reprend du service !
A partir de 1943 les Alliés changent le système de chiffrage pour les agents en utilisant une variante complexifiée du carré de Vigenère, la substitution poly-alphabétique : au lieu d’une clef courte et unique connue de l’opérateur (le poème), la clef sera aussi longue que le message lui-même et changera totalement à chaque message. Après usage elle sera immédiatement détruite (« One time pad ») si bien qu’au cas où l’opérateur serait pris et le matériel saisi personne ne serait capable de déchiffrer le message sauf, bien entendu, le destinataire[9]. Ce principe de chiffrage perdurera jusqu’à l’arrivée des ordinateurs sous des formes diverses avec de plus en plus de complexité et la multiplication des substitutions successives, qui conduira naturellement à la création de machines à coder, le travail à la main devenant très long et fastidieux et source de multiples erreurs.
Pour ce nouveau chiffrage il va falloir utiliser du matériel :
- Un tissu de soie très fin sur lequel est imprimée une grille de chiffrage ;
- Des clefs à utiliser une seule fois, imprimées sur des feuillets: de longues listes de caractères aléatoires.
Voici un morceau de la grille qui comporte normalement 26 lignes et 26 colonnes :
| A | B | C | D | E | F | G | H | I | etc. |
| A o | A e | A m | A h | A a | A q | A i | A c | A l | etc. |
| B m | B o | B l | B s | B i | B f | B r | B z | B u | etc. |
| C w | C s | C u | C f | C x | C p | C t | C a | C o | etc. |
La première ligne représente les lettres de la clef, aussi longue que le message.
Dans les cases en-dessous, la lettre en MAJUSCULE est la lettre du message en clair, la lettre en minuscule est la lettre chiffrée. Par exemple si la lettre-clef est « D » et la lettre en clair est « C », la lettre chiffrée sera : « f ».
Par rapport au carré de Vigenère, la clef change à chaque lettre et ne se répète jamais. De plus la place des lettres de l’alphabet chiffré est aléatoire au lieu d’être seulement décalée. Chaque lettre dispose de 26 substituts possibles, dont elle-même.
Les clefs étaient micro-imprimées sur du papier de riz nitraté très fin qui pouvait s’enflammer instantanément, se dissoudre dans un liquide chaud ou même s’avaler dans danger. Les lettres, toutes petites, ne pouvaient se lire qu’avec une forte loupe. Chaque paquet était composé de 10 feuillets, 5 pour encoder et 5 pour décoder et le tout logeait aisément dans un paquet de cigarettes. Sur chaque feuillet il y avait une longue suite de caractères aléatoires composant la clef.
A chaque utilisation on détruisait la clef. En cas de destruction prématurée ou de manque de feuillets, l’agent pouvait en dernier recours utiliser une clef « poème » convenue à l’avance. Cela ne pouvait être utilisé qu’une seule fois.
Les machines à chiffrer
Quelques considérations
Plus le chiffre est sophistiqué, plus il est long à mettre en œuvre et plus le risque d’erreurs est grand. On s’en est aperçu dès le XVe siècle et on a alors essayé de fabriquer des systèmes mécaniques palliant ces difficultés.
Il est également un autre aspect à considérer : le rapport entre la difficulté du chiffrage et la « durée de vie » d’un message secret avant qu’il ne soit déchiffré. Si le message concerne une opération devant se dérouler dans 2 jours, il faut que le message ne puisse pas être déchiffré en 2 jours. S’il s’agit d’un secret d’état il ne doit pas être révélé avant plusieurs années. Pendant la seconde guerre mondiale les armées allemandes ont utilisé 2 types de machines (les Alliés également). La machine ENIGMA, très répandue servait pour la tactique, la machine de LORENZ réservée à l’élite était utilisée pour la stratégie. La première produit des messages sous forme de lettres transmissibles en morse par exemple, la seconde est un télescripteur qui encrypte les « bits » d’une même lettre. Le cryptage des deux machines fut « cassé » par l’équipe d’Alan Turing à Bletchley Park. Pour cela il utilisa deux machines distinctes, électromécanique pour ENIGMA (les « BOMBES »[10]) et pour LORENZ il fabriqua un système électronique comportant 1500 tubes : le tout premier ordinateur fonctionnel[11] nommé « COLOSSUS ».
La première machine date du XVe siècle sera encore utilisée pendant la seconde guerre mondiale!
La raison en est que cela peut tenir dans la poche et qu’un enfant peut la fabriquer : c’est le disque de Léon ALBERTI.
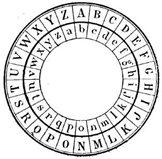
Il s’agit de deux disques concentriques et pivotants (à l’origine en cuivre) présentant un alphabet sur les deux couronnes. L’utilisation comme chiffre de César est évidente : on décale les alphabets et on a immédiatement la lettre en clair à l’extérieur et la lettre encryptée à l’intérieur !
On peut l’utiliser aussi comme carré de Vigenère avec une clef, par exemple « TOM ». Le chiffrage sera alors tri-alphabétique.
- Tourner le disque intérieur et placer le « T » en face du « A ». Repérez la 1e lettre encryptée.
- Tourner le disque intérieur et placer le « O » en face du « A ». Repérez la 2e lettre encryptée.
- Tourner le disque intérieur et placer le « M » en face du « A ». Repérez la 3e lettre encryptée.
Et ainsi de suite jusqu’à la fin du message en répétant la clef « TOM ».

Sur ce principe on peut imaginer quantité de variantes et de présentations. On peut changer le disque intérieur, y placer des symboles, on peut ajouter des chiffres etc. (26 lettres et 10 chiffres représentent 36 cases soit pour la réalisation 10° par case !) Ce disque a été utilisé par les Confédérés pendant la guerre de Sécession mais aussi par les espions allemands en territoire ennemi. En effet on ne peut pas se déplacer discrètement avec une machine ENIGMA tandis qu’un disque peut se réaliser en carton !
La machine ENIGMA ou l’ « ultra Alberti[12] »
Cette machine est un véritable mythe et il faudrait au minimum un article complet pour en parler, explorer son histoire, découvrir la façon dont elle fonctionne et recenser les services rendus pendant le cours de la guerre par son décryptage.
Le fonctionnement n’est pas compliqué à comprendre, mais il est long à expliquer. Il s’agit d’un système mécanique relativement simple (même si la réalisation est du domaine de la précision) et le circuit électrique est des plus élémentaires : on appuie sur une touche et une ampoule électrique s’allume ! Tout le secret est dans la clef qui prend la forme d’un gros livre de codes, car cela change chaque jour.

La photo ci-dessus est celle de la machine à 3 rotors, la plus courante, utilisée par l’armée de terre et l’aviation. La marine a obtenu une machine à 4 rotors.
Le « cœur » de la machine est composé par des rotors dont le principe est celui du disque d’Alberti :
- Sur le flanc droit il y a 26 contacts électriques correspondant aux lettres d’un alphabet « mélangé ».
- Le flanc gauche et également composé de 26 contacts électriques correspondant à un alphabet différent.
- Les deux flancs sont reliés intérieurement par des fils, ce qui réalise une transposition. Chaque rotor est différent et l’opérateur en choisit 3 parmi 5 à disposition, le livre de code indiquant lesquels et dans quel ordre les placer.


- Le premier rotor à droite est en contact avec un circuit d’entrée relié aux touches du clavier. Son flanc gauche est relié au flanc droit du second, même chose pour le 3e.
- Le flanc gauche de celui-ci appuie sur un réflecteur qui réalise une substitution interne et renvoie le courant électrique en sens inverse qui traverse à nouveau tous les rotors pour revenir sur le connecteur d’entrée puis sur le culot d’une ampoule qui s’éclaire.
- Entre temps le signal traverse ou non des connecteurs de substitution qui sont de simple fils : par exemple tous les « W » deviennent systématiquement des « J » et inversement.
Essayons de comptabiliser les substitutions pour une seule lettre :
- Connecteur d’entrée -> rotor
- 1er rotor entre ses flancs
- Contact entre 1er et 2e rotor
- 2e rotor entre ses flancs
- Contact entre 2e et 3e rotor
- 3e rotor entre ses flancs
- Contact 3e rotor avec réflecteur
- Réflecteur en interne
- Et l’on repart en sens inverse !

Cela fait 8 à l’aller, 7 au retour soit 15 substitutions plus celles aléatoires des cordons, donc l’équivalent au minimum de 15 disques d’Alberti pour une seule lettre à chiffrer! En effet la combinaison change à chaque lettre car les rotor tournent… ou ne tournent pas ! Le premier rotor tourne à tous les coups, les autres selon le codage choisi.
La clef d’ENIGMA est dans le livre de codes, bien plus important que la machine elle-même qui était connue depuis longtemps par les services secrets alliés.
Voici un exemple tiré d’un livre d’octobre 1944.

Datum : La date en ordre inverse. On peut ainsi découper et détruire les lignes périmées.
Walsenlage : Les rotors à utiliser et dans quel ordre.
Ringstellung : Position de l’anneau qui commande la rotation des rotors 2 et 3.
Steckerverbindungen : Mise en place des cordons de substitution.
Kenngruppen : Position de départ des rotors.
Quand on a respecté les consignes on tape les lettres du message en clair. A chaque frappe une lettre s’éclaire, c’est la lettre encryptée. Il faut bien noter sinon il faut tout refaire depuis le début.
Il y a parfois une procédure supplémentaire. Exemple de message reçu
U6Z DE C 1510 = 44 = EHZ TBS =
VQDKV FNPYW DEWEQ GVSUO YHPHL =
On remarque la présence de trigrammes dans l’en-tête, deux groupes de 3 lettres alors que le message est envoyé par groupes de 5 lettres.
- Régler la machine comme indiqué dans le livre de codes
- Placer les rotors en position donnée par le premier trigramme : EHZ
- Décoder le second trigramme : TBS et noter les lettres obtenues par exemple : KUC
- Positionner les rotors de cette façon et continuer le déchiffrage.
Nous n’irons pas plus loin dans l’étude de cette machine, ce serait trop long.
La machine de Lorenz

C’est un télescripteur très performant qui utilise le chiffrement par flux encore utilisé pour nos communications WI-FI ou Bluetooth.
En télégraphie Baudot (Télétype ou Radio-télétype) les lettres sont codées sur 5 bits. La machine de Lorenz produit des bits pseudo aléatoires et les combine avec le texte en clair par un « OU exclusif » (XOR).
Dès avril 1943 le chiffre de ces machines réservées à l’élite hitlérienne fut « cassé ». L’ordinateur « Colossus » opérationnel en décembre de la même année permit d’effectuer les opérations rapidement.
| A | B | XOR |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Exemple d’encryptage :
La lettre « A » en code Baudot porte le numéro 24 en numération décimale soit 11000 en numération binaire. Si la machine génère le code 10101b[13] le résultat du OU exclusif sera : 01101b soit 13 en décimal. Cela correspond à la lettre « G ».
L’opération est réversible pour le décryptage. Si les réglages de la machine sont identiques les mêmes codes seront générés. Si l’on effectue 01101b EXOR 10101b le résultat sera 11000b, soit 24 en décimal, la lettre « A ».
Avec cette machine (et ses semblables chez les Alliés) on abandonne l’écriture « humaine » pour celle des machines. En effet jusqu’à ENIGMA on a traité des alphabets classiques même s’ils sont parfois codés, remplacés par des symboles. Maintenant on parle d’opérations mathématiques, de fichiers numérisés ne comportant que des 1 et des 0. Le disque d’Alberti, ENIGMA étaient des « prothèses » pour rendre nos actions plus fiables et plus rapides. Maintenant ce sont les machines qui communiquent entre elles dans leur propre langage. Notre rôle est de les interfacer pour que nous puissions les comprendre. Certains y verront une emprise de la machine sur l’homme. On peut seulement dire que nous avons contracté une addiction et qu’elles nous sont devenues indispensables. Mais ce n’est pas parce que nous utilisons l’odorat des chiens pour trouver des truffes (et bien d’autres choses) que nous vivons sur « la planète des chiens » !
Les machines de l’après-guerre.

Elles ont été utilisées par toutes les armées, dont l’armée française. Il y en a de deux sortes : les descendantes d’ENIGMA et celles de LORENZ avec des principes identiques et pour les mêmes usages.
Elles ont pour noms C-35, C-36, C-37, C-52, BC-243 et bien d’autres ! Le créateur de beaucoup de ces machines est l’industriel suédois Boris Hagelin. (Photo ci-contre : C-36)
En recherchant d’autres modèles voici ce que l’on peut trouver sur WIKIPEDIA :
| A rotors | ENIGMA, Fialka, Hebern, HX-63 KL-7, M-325, NEMA, SIGABA, Typex |
| Mécaniques | Cylindres :Bazéries ou Jefferson, C-52, CD-57, HC-9, Kryha, M-94, M-209, C-36, Scytale |
| Téléscripteurs | 5-UCO, BID 770, KW-26, KW-37, LORENZ, T52, TAREC |
| Autres | Cryptex, KG-84, JADE |
Sur la même encyclopédie en ligne vous aurez des informations sur la plupart d’entre-elles si cela vous intéresse, mais bien qu’elles soient très largement dépassées cela reste dans le domaine de la discrétion.
Et depuis lors le chiffre se porte de mieux en mieux !
Actuellement notre société entière est sujette en permanence aux « identifications » et « mots de passe » si bien que « login » et « password » sont désormais connus de tous les Français. Il faudrait en changer très souvent et ne pas utiliser le même pour des services différents mais cela devient vite un casse-tête. Les filous sont passés maîtres dans l’art de les voler par la ruse et il faut être vraiment attentif pour ne pas cliquer au mauvais endroit sur un message INTERNET. Le piratage des hôpitaux ou des entreprises en vue de les rançonner en est une bonne illustration.
On peut également parler des algorithmes de compression des données informatiques : zip, tar, etc.
Il est certain que les nouveaux chiffrages sont effectués à partir d’ordinateurs dont la puissance de calcul est de plus en plus grande avec des clefs de plus en plus longues !
Il y a quelques décennies il y avait un problème avec la diffusion de la clef entre partenaires, tout comme les Allemands avaient des difficultés à préserver le secret de leurs livres de codes. Elles étaient transmises par valise diplomatique ou par des porteurs anonymes et discrets ! Désormais il existe des « clefs publiques » ! Expliquons cela. Est-ce simple ? Non, vous êtes prévenus…
Le procédé qui transforme une expression mathématique en une autre est appelée « fonction ». Une addition, une multiplication sont des fonctions réversibles, comme par exemple U=R x I qui peut être aussi : I = U / R etc. Jusqu’alors les transformations d’alphabets étaient réversibles, symétriques comme nous venons d’en parler à propos de la machine de LORENZ.
Certaines fonctions sont irréversibles comme la fonction MODULO qui est le reste de la division euclidienne. Exemple 11 : 3 = 9 reste 2. Le modulo de 11 par 3 est 2. Examinons les résultats de 2 fonctions :
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| 3x | 3 | 9 | 27 | 81 | 243 | 729 |
| 3x (mod 7) | 3 | 2 | 6 | 4 | 5 | 1 |
Alors que 3 « puissance x » présente une progression régulière et peut être retournée par la fonction « racine », la suite des modulos semble aléatoire et ne permet pas de retrouver l’origine de l’opération car il y a une infinité de divisions euclidiennes qui ont le même reste. On peut écrire de façon générale la formule utilisée ci-dessus:
Y x (mod P)
Voici un exemple illustrant la démarche entre une banque et sa succursale pour échanger une clef simpliste, un seul nombre comme pour le chiffre de César. L’intérêt est de transmettre la clef de manière sécurisée, même si la communication est espionnée par un concurrent.
- La banque et la succursale gardent chacune un chiffre secret, 3 pour la banque et 6 pour la succursale. Ils seront le « x » de la formule, la puissance élévatrice. Les deux peuvent se téléphoner pour communiquer les valeurs communes de Y et P de la formule ci-dessus, par exemple Y=7 et P=11 , la valeur de « x » restant secrète de part et d’autre ;
- Les partenaires appliqueront alors la formule : 7x(mod 11) c’est à dire 73(mod 11) pour la banque et 76(mod 11) pour la succursale, les résultats étant respectivement 2 et 4 ;
- Ils peuvent se les communiquer sans crainte car ce n’est pas la clef ;
- La banque applique la formule : 43(mod 11) = 9 ;
- La succursale applique la formule : 26(mod 11) = 9.
9 est la clef qui a été transmise grâce à des chiffres inutilisables par les espions !
Il suffit d’une calculette pour obtenir ce résultat, alors avec des ordinateurs…
Et en conclusion : l’avenir… peut-être…
Il s’agit peut être de « l’intrication quantique ». C’est un phénomène (démontré) dans lequel deux particules sont liées et présentent des états quantiques dépendants sans qu’aucune liaison matérielle ne les relie. Si l’état quantique de l’une change, l’état quantique de l’autre également quelle que soit la distance entre elles. Ce serait très commode pour échanger des clefs de cryptage !
Pour le moment, et même si l’on a réussi à expérimenter le système, la distance reste très faible, au plus quelques mètres. Mais cela progressera certainement.
Alain CAUPENE (F5RUJ)
Bibliographie :
- Histoire des codes secrets. Simon SINGH (JC LATTES)
- Armement clandestin France. Pierre LORAIN (Auteur)
- ENIGMA (version française). Colonel Frederick WINTERBOTHAM (LAFFONT)
- Agent secret de Churchill. Robert MALOUBIER (TALLANDIER)
- Encyclopédie WIKIPEDIA
- Divers sites INTERNET
[1] Ou « Demaratus ». Ancien roi de Sparte rival de Cléomène déchu et exilé en Perse. Un agent double ?
[2] Léonidas 1er roi de Sparte, successeur de Cléomène est mort à la bataille des Thermopyles.
[3] Le poète André Breton a été le théoricien du surréalisme.
[4] Kenngruppenbuch
[5] Blaise Vigenère (1523–1596) : Diplomate, mathématicien, cryptographe, astronome, astrologue…
[6] Charles Babbage, scientifique anglais (1791 – 1871), mathématicien et inventeur de la « machine analytique » portant son nom est le précurseur de l’informatique.
[7] Félix Marie Delastelle (1840-1902) : « Traité élémentaire de cryptographie ».
[8] Le poème de Violette Szabo dite « Louise » est rapporté par Bob Maloubier, un équipier de la mission SALESMAN, dans son ouvrage : « Agent secret de Churchill ». Après la guerre il participera à la refondation des services de renseignements français et sera le créateur de l’unité des plongeurs de combat.
[9] Voir « Armement clandestin » de Pierre Lorain.
[10] Qualifiées de « déesses de bronze » par le colonel Winterbotham (alors capitaine) qui publiera : « The Ultra secret » en 1974, après la levée du secret.
[11] La machine analytique de Babbage n’a jamais été terminée faute de crédits.
[12] Pour ne révéler à personne que l’on décryptait les messages d’ENIGMA, les informations obtenues étaient dites issues de la « source ULTRA ».
[13] Le « b » indique qu’il s’agit d’un nombre binaire.